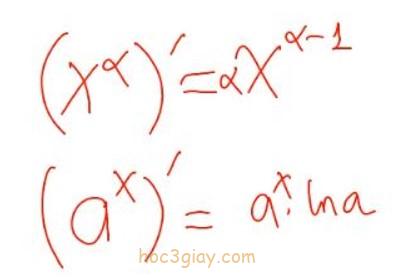Cách làm bài tập vi phân toàn phần cấp 1 và cấp 2

Trong bài viết hôm nay thì bạn sẽ cùng với mình đi tìm hiểu cách làm bài tập vi phân toàn phần cấp 1 và cấp 2 nhé. Mời các bạn theo dõi bên hướng dẫn chi tiết bên dưới đây.

Cách làm bài tập vi phân toàn phần cấp 1 và cấp 2

Vi phân toàn phần cấp 1

Tóm tắt lý thuyết:

Ví dụ: Cho hàm f(x,y) = 3^x/y. Tính df(1,1).

Bước 1: Như yêu cầu đề bài ta có df(1,1) = d^‘_x(1,1)dx + d^‘_y(1,1)dy. Vì vậy ta trước phải đi tính đạo hàm riêng theo biến x và y của hàm f(x,y) = 3^x/y tại x = 1, y = 1.

Công thức đạo hàm đặc biệt

Ta có:

f^‘_x(x,y) = 3^x/y.ln(3).(x/y)^‘_x = 3^x/y.ln(3).(1/y) => f^‘_x(1,1) = 3ln(3)

f^‘_y(x,y) = 3^x/y.ln(3).(x/y)^‘_y = 3^x/y.ln(3).(-1)xy^-2 => f^‘_y(1,1) = -3ln(3)

Bước 2: Thay vào công thức tổng quát ta được kết quả cuối cùng là:

Vậy df(x,y) = f^‘_x(x,y)dx + f^‘_y(x,y)dy = 3ln(3)dx – 3ln(3)dy = 3ln(3)(dx – dy).

Vi phần toàn phần cấp 2

Tóm tắt lý thuyết:

Ví dụ: Tìm vi phân cấp 2 của hàm z = e^xy tại M₀(1,2).

Bước 1: Ta đạo hàm riêng hàm z = e^xy đến cấp 2

Xem công thức đạo hàm: Tại đây

Đạo hàm riêng cấp 1:

f^‘_x(x,y) = e^xy.ln(e).(xy)^‘_x = e^xy.ln(e).y = e^xy.y

f^‘_y(x,y) = e^xy.ln(e).(xy)^‘_y = e^xy.ln(e).x = e^xy.x

Đạo hàm riêng cấp 2:

f^”_xx(x,y) = e^xy.y.ln(e).(xy)^‘_x = e^xy.y.ln(e).y = e^xy.y² => f^”_xx(1,2) = 4e²

f^”_xy(x,y) = (e^xy)^‘_y.y + e^xy.(y)^‘_y = e^xy.ln(e).(xy)^‘_y.y + e^xy = e^xy.ln(e).x.y + e^xy = e^xy.x.y + e^xy => f^”_xy(1,2) = 2.e² + e² = 3e²

f^”_yy(x,y) = e^xy.x.ln(e).(xy)^‘_y = e^xy.x.ln(e).x = e^xy.x² => f^”_xx(1,2) = e²

Bước 2: Thay vào công thức tổng quát ta được kết quả cuối cùng là:

Vậy d²f(1,2) = 4e²dx² + 2.3e².dxdy + e²dy² = e²(4dx² + 6dxdy + dy²).