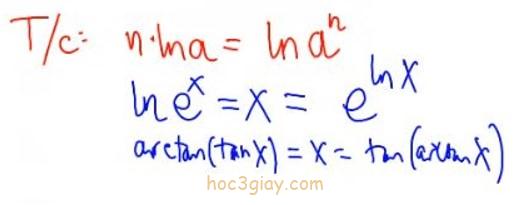Trong bài viết hôm nay thì mình và các bạn sẽ cùng nhau đi tìm hiểu về cách làm bài tập phương trình vi phân tuyến tính cấp 1. Mời mọi người theo dõi phần hướng dẫn chi tiết bên dưới đây nhé.
Cách làm bài tập phương trình vi phân tuyến tính cấp 1
Tóm tắt lý thuyết:
Trong phương trình vi phân tuyến tích nó sẽ chia ra làm 2 dạng gồm: Dạng [L] và [H], chúng ta sẽ đi với dạng thứ nhất dạng [H] ngay phía bên dưới.
Phương trình vi phân tuyến tính cấp 1 dạng [H]
Như trong phần tóm tắt lý thuyết phía trên ta đã biết được dạng [H] có phương trình là: y‘ + p(x)y = 0 với tên gọi là PTTT thuần nhất và nghiệm của [H] ở dạng: yTQ = Ce-∫p(x)dx
Bây giờ chúng ta sẽ làm ví dụ sau.
Ví dụ: y‘ + 2(y/x) = 0
Bước 1: Chuyển phương trình đề cho về dạng [H] là y‘ + p(x)y = 0.
y‘ + 2(y/x) = 0
<=> y‘ + (2/x).y = 0 có dạng [H] với p(x) = 2/x
Bước 2: Dùng công thức tính nghiệm TQ của dạng [H] là yTQ = Ce-∫p(x)dx để tính ra kết quả cuối cùng.
Nghiệm TQ là:
yTQ = Ce-∫p = C.e-∫(2/x)dx = C.e-2∫(1/x)dx = C.e-2.lnx = C.elnx^(-2) = C.x-2 = C/x2, C ∈ R.
Một số tích chất cần nhớ
Phương trình vi phân tuyến tính cấp 1 dạng [L]
Như trong phần tóm tắt lý thuyết phía trên ta đã biết được dạng [L] có phương trình là: y‘ + p(x)y = f(x) và nghiệm của [L] ở dạng: yTQ = φ(x)e–∫p(x)dx = φ(x)/e∫p(x)dx
Bây giờ chúng ta sẽ làm ví dụ sau.
Ví dụ: y‘ – y/x = 3x3
Bước 1: Chuyển đổi về dạng [L] là y‘ + p(x)y = f(x).
y‘ – y/x = 3x3
<=> y‘ + (-1/x).y = 3x3 có dạng [L] với p(x) = -1/x, f(x) = 3x3
Bước 2: Ta đi tìm nghiệm tổng quát nhờ công thức tính nghiệm TQ của dạng [L] là yTQ = φ(x)/e∫p(x)dx.
Nghiệm TQ của [L]: yTQ = φ(x)/e∫p
Mà: e∫p = e∫-1/x.dx = e–∫1/x.dx = e-lnx = elnx^(-1) = x-1 = 1/x
φ‘ = f(x).e∫p = 3x3.(1/x) = 3x3/x = 3x2
=> φ = ∫φ‘ = ∫3x2dx = x3 + C
Bước 3: Kết luận
Vậy yTQ = (x3 + C)/(1/x) = x(x3 + C), C ∈ R.
