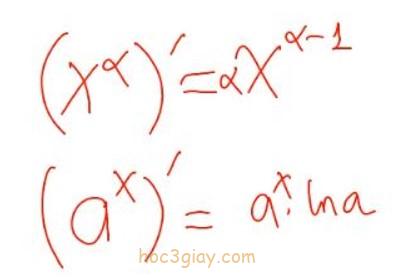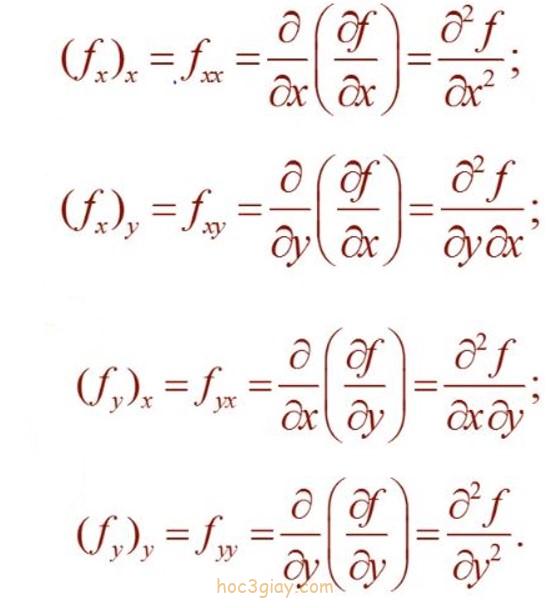Trong bài viết này thì mình sẽ hướng dẫn cho các bạn một trong những bài toán quan trọng nhất đó là đạo hàm riêng. Đạo hàm riêng là một phần rất được sử dụng nhiều vậy nên là bạn hãy cùng làm quen nó ngay trong bài viết này nhé. Mời các bạn theo dõi bên dưới.
Cách làm bài tập đạo hàm riêng cấp 1 và cấp 2
Chú ý: Để tính đạo hàm riêng theo biến x, ta xem y là hằng số và ngược lại.
 Đạo hàm riêng cấp 1
Đạo hàm riêng cấp 1
Cho ví dụ: Cho hàm f(x,y) = 3x2y3 – 4xy2 + 5xy – 7x + 8y – 1 và điểm M(1, -1). Tìm f‘x(M).
Bài làm:
Bước 1: Ta thấy rằng đề đang yêu cầu tìm đạo hàm riêng theo biết x, vậy nên ta sẽ xem y là hằng số. Mà đề bài đã cho y là -1, giờ ta sẽ thay y = -1 vào đề nhé.
Ta có f(x, -1) = -3x2 – 4x – 5x -7x – 8 – 1
= -3x2 – 16x – 9
Bước 2: Ta đạo hàm riêng biến x cho hàm số -3x2 – 16x – 9
=> f‘x(x, -1) = -6x – 16
Bước 3: Thay x = 1 như yêu cầu của đề bài
=> f‘x(M) = f‘x(1, -1) = -22
Tương tự cách làm khi yêu cầu đề bài bắt làm đạo hàm theo biến y, đến lúc đấy ta sẽ xem x là hằng số.
Các trường hợp đặt biệt:
Trường hợp đặc biệt
Đạo hàm riêng cấp 2
Cho ví dụ: Tính các ĐHR cấp 2 của hàm: f(x,y) = x2y3 + x4.
Bước 1: Đạo hàm riêng cấp một theo biến x và biến y
Ta có: f‘x(x,y) = 2xy3 + 4x3 ; f‘y(x,y) = x2.3y2 + 0
Bước 2: Đạo hàm tiếp cho hàm số 2xy3 + 4x3 và x2.3y2 + 0 theo 2 biến x và y ta sẽ có được f”xx, f”xy, f”yx, f”yy.
f”xx = (2xy3 + 4x3)‘x = 2y3 + 12x2
f”xy = (2xy3 + 4x3)‘y = 6xy2 + 0
f”yx = (x2.3y2)‘x = 6xy2
f”yy = (x2.3y2)‘y = 6x2y
Bởi vì theo định lý Clairaut: Nếu f(x,y) có các ĐHR hỗn hợp fxy và fyx trong lân cận U của M(a,b) và chúng liên tục trên U thì: fxy(M) = fyx(M).
Như vậy khi ta làm bài đạo hàm riêng cấp 2, bạn có thể chỉ cần viết 3 cái là f”xx, f”xy, f”yy hoặc f”xx, f”yx, f”yy. Vì fxy và fyx có đáp án là giống nhau.
 Lời kết
Lời kết
Qua bài viết cách làm bài tập đạo hàm riêng cấp 1 và cấp 2 này thì bạn đã nắm vững được về đạo hàm riêng cấp 1 và cấp 2 chưa nào. Chúc các bạn có thể học thật tốt và hẹn gặp lại ở các bài viết tiếp theo.