Cách làm bài tập phương trình vi phân tuyến tính cấp 2

Trong bài viết ngày hôm nay bạn và mình sẽ cùng nhau đi tìm hiểu cách làm bài tập phương trình vi phân tuyến tính cấp 2. Mời các bạn xem phần hướng dẫn chi tiết bên dưới đây.

Cách làm bài tập phương trình vi phân tuyến tính cấp 2

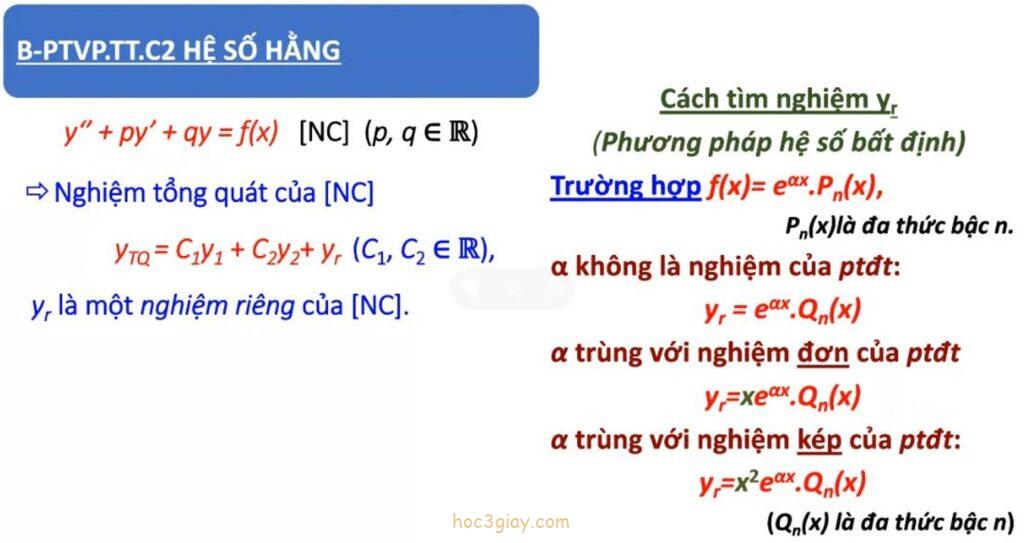
Tóm tắt lý thuyết:

Phương trình vi phân tuyến tính dạng HC

Vi dụ: Tìm nghiệm tổng quát của PTVP y^” – 5y^‘ + 4y = 0.

Bước 1: Ta xác định dạng của PTVP đề bài và xét phương trình đặc trưng của nó.

y^” – 5y^‘ + 4y = 0 có dạng [HC]. Xét phương trình đặc trưng ứng với λ² – 5λ + 4 = 0 có nghiệm: λ₁ = 4, λ₂ = 1.

Bước 2: Xét các trường hợp trong phần lý thuyết bên trong bức ảnh trên để tìm nghiệm cơ bản của dạng [HC].

Vì λ₁ ≠ λ₂ phương trình đặc trưng có 2 nghiệm cơ bản là: y₁ = e^4x; y₂ = e^x

Bước 3: Thay vào công thức tính nghiệm tổng quát của [HC].

Nghiệm tổng quát là: y_TQ = C1.e^4x + C2.e^x, C1,C2 ∈ R.

Phương trình vi phân tuyến tính dạng NC

Ví dụ: Tìm một nghiệm riêng của phương trình y^” + y^‘ – 6y = x².e^-2x

Bước 1: Chuyển PTVP đề bài cho thành PT đặc trưng và tìm nghiệm λ_1, λ₂.

y^” + y^‘ – 6y = x².e^-2x có dạng [NC]. Xét phương trình đặc trưng ứng với λ² + λ – 6 = 0 có nghiệm: λ₁ = 2, λ₂ = -3.

Bước 2: Xác định α và p_n(x).

Nhận xét: f(x) = e^-2x .x²

Có:

α = -2 không là nghiệm của PT đặc trưng (nghiệm phương trình đặc trưng vừa tính là λ₁ = 2, λ₂ = -3)

p_n(x) = x² là đa thức bậc 2.

Bước 3: Thay vào công thức tính nghiệm riêng phù hợp y_r.

=> y_r = e^-2x.[ax² +bx + c]